[KALKULUS] TURUNAN FUNGSI IMPLISIT
FUNGSI IMPLISIT
Fungsi implisit adalah fungsi yang terdiri dari dua atau lebih variabel yang terdiri dari variabel bebas dan variabel tak bebas, yang berada dalam satu ruas dan tidak dapat diselesaikan pada ruas yang berbeda.
Menurunkan fungsi implisit, mengambil jauh berbeda dengan penurunan fungsi variabel tunggal, yaitu dengan menggunakan notasi Leibniz (dy / dx). Berikut ini, hal yang harus diselesaikan di dalam fungsi Implisit yang memiliki dua variabel (x dan y).
fungsi-fungsi Implisit
Persamaan f (x, y) = 0 pada suatu daerah tertentu, tentukan y sebagai fungsi implisit dari x, maka turunan y dapat ditentukan sbb:
Jika mungkin ubalah fungsi implisit, menjadi fungsi eksplisit y = g (x), kemudian dibedakan.
Pikirkan y sebagai fungsi x, kemudian turunkan persamaan tersebut terhadap x dan persamaan yang diperoleh agar dipecahkan untuk y '
Turunan Implisit
Turunan implisit ditentukan berdasarkan variabel yang terdapat dalam fungsi.
Suatu fungsi dengan variabel x, turunannya : x d/dx.
uatu fungsi dengan variabel y, turunannya : y d/dy. dy/dx.
Suatu fungsi dengan variabel x dan y, turunannya : xy d/dx + xy d/dy . dy/dx.
Agar lebih memaham mengenai turunan, coba kerjakan soal berikut kemudian periksalah jawaban kalian dengan menggunakan pembahasan pada bagian di bawah ini.
Contoh Soal Turunan
1. Tentukan turunan dari fungsi berikut.
- f(x) = 8
- g(x) = 3x + 5
- h(x) = 6x3
- k(x) = 3x5/3
- m(x) = (3x2 + 3)4
Pembahasan
- f’(x) = 0
- g’(x) = 3
- h’(x) = 6 (3) x3 – 1 = 18x2
- k’(x) = 3 (5/3) x(5/3) – 1 = 5x2/3
- m’(x) = 4 . (3x2 + 3)4 – 1 . 6x = 24x . (3x2 + 3)3
2. Tentukan turunan dari fungsi berikut.
f(x) = (3x + 2) . (2x2 – 1)
Pembahasan
Misal: u(x) = 3x + 2 dan v(x) = 2x2 – 1
f’(x) = u’(x) . v(x) + u(x) . v’(x)
f’(x) = 3 . (2x2 – 1) + (3x + 2) . (4x)
f’(x) = 6x2 – 3 + 12x2 + 8x = 18x2 + 8x – 3
3. Diberikan sebuah fungsi ordo 2 seperti di bawah ini
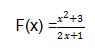
Tentukan nilai f(0) + 3f’(1)
Pembahasan
Untuk mengerjakan soal ini, kita dapat memasukkan nilai 0 ke dalam fungsi tersebut.
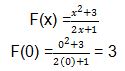
Setelah Anda, mendapatkan nilai f(0). Kita dapat mengerjakan turunan fungsi hasil bagi menggunakan salah sifat turunan.
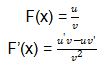
Untuk menggunakan rumus tersebut, kita dapat menggunakan pemisalan dan turunannya seperti di bawah ini.
U = x2 + 3 ; U’ = 2x
V = 2x + 1 ; V’ = 2
Kemudian, kita bisa memasukkan pemisalan tersebut ke dalam rumus turunan yang sebelumnya serta kita dapat secara langsung memasukkan f’x(1).
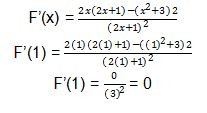
Maka, hasil f(0) + 3f’(1) = 3 + 3(0) = 3
4. Tentukan hasil turunan f(x) = (x2 + 2x + 3)(3x + 2)
Pembahasan
Sama seperti soal sebelumnya, Untuk mengerjakan soal turunan dalam bentuk perkalian, kita dapat menggunakan rumus sifat turunan serta menggunakan pemisalan dalam fungsi tersebut seperti di bawah ini.
F’(x) = u’v + uv’
U = x2 + 2x + 3 ; U’ = 2x + 3
V = 3x + 2 ; V’ = 3
F’(x) = u’v + uv’
F’(x) = (2x+3)(3x + 2) + (x2 + 2x + 3)(3)
F’(x) = 6x2 + 13x + 6 + 3x2 + 6x + 9
F’(x) = 9x2 + 19x + 15
Sehingga bentuk akhir F’(x) adalah 9x2 + 19x + 15
Jika terdapat f(x) = (2x-1)2(x+2). Berapakah nilai f’x(2)
Pembahasan
Untuk mengerjakan soal ini, kita bisa menggunakan sifat turunan fungsi f’(x) = u’v + v’u untuk mendapatkan hasil akhir. Sehingga kita dapat melakukan pemisalan kembali.
F’(x) = u’v + uv’
U= (2x-1)2 = 4x2 – 4x + 1 ; U’ = 8x – 4
V = x + 2 ; V’ = 1
F’(x) = u’v + uv’
F’(x) = (8x – 4)(x + 2) + (4x2 – 4x + 1)(1) ; kita dapat memasukkan nilai 2 seperti di soal
F’(2) = ((8(2) – 4)(2 + 2)) + ((4(2)2 – 4(2) + 1)(1))
F’(2) = ((16-4)(4)) + ((16-8+1)(1))
F’(2) = 96 + 9 = 105
Sehingga nilai akhir F’(2) adalah 105
Contoh-contoh:
Selesaikan diferensiasi fungsi dimasukkan ke dalam turunan pertama dan ke dua
xy + x - 2y - 1 = 0
xy - x + y - 2 = 0
y 2 = 2x 3
x 2 + 5t 2 = 1
x 3 + x 2 y - 10y 4 = 0
Penyelesaian.
1. Ubah fungsi tersebut ke dalam fungsi eksplisit lalu turunkan
xy + x - 2y - 1 = 0
(x - 2) y = 1 - x
y = y '= =
y '= =
xy - x + y - 2 = 0
xy - y = 2 + x
(x + 1) y = 2 + x
y =
y '=
y '= y' =
3. y 2 = 2x 3 Persamaan tetap dalam fungsi implisit
d / dx (y 2 ) = d / dx (2x 3 )
2 y y '= 6 x 2
y '= 6x 2 / 2y y' = 3x 2 / y. 2thn ¹ 0
4. x 2 + 5y 2 = 1
d / dx (x 2 ) + d / dx (5y 2 ) = d / dx (1)
2x + 10yy '= 0
y '= - 2x / 10y atau y' = - x / 5y. y ¹ 0
5. x 3 + x 2 y - 10y 4 = 0
d / dx (x 3 ) + d / dx (x 2 y) - d / dx (10y 4 ) = d / dx (0)
3x 2 + 2xy + x 2 y '- 40y 3 y' = 0
40y 3 y '- x 2 y' = 3x 2 + 2xy
(40y 3 - x 2 ) y '= 3x 2 + 2xy
y '=
2. Derivativ Tingkat Tinggi Fungsi Implisit
Misalnya y = f (x), fungsi x yang dapat membedakan dan turunnnya disebut turunan pertama, jika hasil turunan ini dikumpulkan lagi hingga ketingkat yang lebih tinggi, maka disebut diferensiasi tingkat tinggi.
Turunan dari orde disuatu titik hanya mungkin ada jika dari turunan lebih rendah dapat didiferensiasikan di titik tersebut.
Misal y = f (x)
Turunan Berlanjut: y '= dy / dx = f' (x)
Turunan antara: y ”= d 2 y / dx 2 = f” (x)
Turunan ketiganya: y '' '= d 3 y / dx 3 = f' '' (x)
Turunan ke-n: y n = d n y / dx n = f n (x) …… ..dst.
Contoh-contoh:
1. Carilah turunan ke 4nya fungsi y = 5x 4 - 4x 3 + 3x 2 - 2x + 1
Jawab: y '= 20x 3 - 12x 2 + 6x - 2
y ”= 60x 2 - 24x + 6
y '' '= 120x - 24
y 4 = 120
2. Carilah Turunan kedua dari fungsi xy + 2x - 4y = 10
Jawab: d / dx (xy) + d / dx (2x) - d / dx (4y) = d / dx (10)
y + xy '+ 2 - 4y' = 0 atau x y '- 4 y' = - 2 - y
(x - 4) y '= - (2 + y) y' =
dari y + xy '+ 2 - 4y' = 0 kita turunkan lagi
d / dx (y) + d / dx (x y ') + d / dx (2) - d / dx (4y') = d / dx (0)
y '+ y' + xy ”- 4y” = 0
2 y '+ (x - 4) y ”= 0
(x - 4) y “= - 2 y '
(x - 4) y ”= - 2 ()
(x - 4) y “=
y ”=
Hitung y 'dan y ”pada x = 1 dan y = -1 untuk fungsi x 3 y + xy 3 = 2
Jawab:
d / dx (x 3 y) + d / dx (xy 3 ) = d / dx (2)
3x 2 y + x 3 y '+ y 3 + 3 xy 2 y' = 0
x 3 y '+ 3 xy 2 y' = - (3 x 2 y + y 3 )
(x 3 + 3 xy 2 ) y '= - (3x 2 y + y 3 )
y '=
untuk x = 1 dan y = -1 kita masukkan harga tersebut ke y 'maka diperoleh y' = 1
untuk y ”dari 3x 2 y + x 3 y '+ y 3 + 3 xy 2 y' = 0 kita turunkan lagi
d / dx (3x 2 y) + d / dx (x 3 y ') + d / dx (y 3 ) + d / dx (3xy 2 y') = 0
6xy + 3 x 2 y '+ 3 x 2 y' + x 3 y ”+ 3 y 2 y '+ 3 y 2 y' + 6 xy y'y '+ 3 xy 2 y” = 0
x 3 y ”+ 3x y 2 y” = - 6 xy - 6 x 2 y '- 6 y 2 y' - 6 xy y ' 2
(x 3 + 3 xy 2 ) y ”= - (6 xy + 6 x 2 y '+ 6 y 2 y' + 6 xy y ' 2 )
y “=
untuk x = 1, y = -1 dan y '= 1, didapat y ”= 0
3. Nilai Extrem.
Suatu nilai ekstrem fungsi akan titik kritis, fungsi naik dan fungsi nilai maksimum dan minimum fungsi.
Menentukan titik kritis;
Jika f (x) dapat diterima dalam selang a £ x £ b dimana f (x) memiliki nilai relatif maka f '(x) = 0 adalah kritis
Selesaikan f '(x0) = 0 untuk harga-harga kritis. Buat garis bilangan y 'untuk harga-harga kritis tentukan tanda setiap ruas dari y'.
4. Fungsi Naik & Fungsi Turun
Naik fungsi x = x 0 . bila turunannya positif, f '(x 0 ) > 0.
Saat fungsi diminta pada x = x 0 , jika turunannya negatif, f '(x 0 ) < 0.
Saat fungsi diberikan diam (stationer) pada x = x 0 , jika turunannya nol, f '(x 0 ) = 0.
5 Harga Maksimum dan Minimum.
Suatu fungsi f (x) bernilai maksimum, jika f '(x 0 ) mengubah tanda dari tanda positif menjadi negatif.
Suatu fugnsi f (x) bernilai minimum, jika f '(x 0 ) mengubah tanda dari tanda negatif ke positif.
Komentar
Posting Komentar