[KALKULUS] LIMIT TRIGONOMETRI

-

Limit Trigonometri 

Saya Zulfi Rafidhoh Hikmi, mahasiswa Institut Teknologi PLN. di Blog ini saya akan berbagi ilmu sedikit tentang Limit Trigonometri pada blog ini juga saya buat untuk memenuhi tugas mata Kuliah Kalkulus.selamat berlajar guuys.

Pengertian Limit Trigonimetri

Limit trigonometri adalah nilai terdekat suatu sudut pada fungsi trigonometri. Perhitungan limit fungsi trigonometri bisa langsung disubtitusikan seperti limit fungsi aljabar tetapi ada fungsi trigonometri yang harus diubah terlebih dahulu ke identitas trigonometri untuk limit tak tentu yaitu limit yang apabila kita langsung subtitusikan nilai nya bernilai 0, atau bisa juga untuk limit tak tentu tidak harus memakai identitas tetapi memakai teorema limit trigonometri dan ada juga yang memakai identitas dan teorema. Jadi, apabila suatu fungsi limit trigonometri di subtitusikan nilai yang paling mendekati nya menghasilkan dan maka kita harus menyelesaikan dengan cara lain.
Dalam menentukan nilai limit suatu fungsi trigonometri terdapat berbagai cara yang bisa dipakai :
  • Metode Numerik
  • Subtitusi
  • Pemfaktoran
  • Kali Sekawan
  • Menggunakan Turunan
Penulisan nya dapat ditulis  sebagai berikut :
lim┬( x→c )⁡f( x )
Cara untuk membaca dari limit di atas yaitu limit fungsi f( x ) untuk x mendekati c.

Berbagai Macam – Macam Trigonometri dan singkatan nya

A. Macam – macam trigonometri
Berikut ini adalah nama – nama trigonometri yang biasa kita gunakan :
  • Sinus ( sin )
  • Tangen ( tan )
  • Cosinus ( cos )
  • Cotongen ( cot )
  • Secan ( sec )
  • Cosecan ( Csc )
B. Rumus kebalikan dalam trigonimetri
  • sin⁡∝ = 1/csc⁡∝
  • cos⁡∝ = 1/sec⁡∝
  • tan⁡∝ = 1/cot⁡∝
  • tan⁡∝ = sin⁡∝/cos⁡∝
  • cot⁡∝=cos⁡∝/sin⁡∝
C. Identitas Trigonometri dalam trigonimetri
Sin2⁡∝ + cos2⁡∝ =1
1+cot2⁡∝=csc2⁡∝
Tan2⁡∝+1=sec2⁡∝
D. Rumus Jumlah dan Selisih dalam trigonimetri

E. Rumus Perkalian dalam trigonimetri
F. Rumus sudut rangkap dalam trigonimetri

Teorema Limit Trigonometri

Ada beberapa teorema yang dapat digunakan untuk menuntaskan persoalan limit trigonometri yaitu sebagai berikut ;

Teorema A

Teorema tersebut hanya berlaku pada saat (x -> 0) .

Teorema B

Terdapat beberapa teorema yang berlaku. Untuk setiap bilangan real ( asli ) “c” di dalam daerah asal fungsi yaitu :
Biasanya dalam sebuah soal limit fungsi trigonometri nilai terdekat dari limit fungsi nya yaitu berupa sudut – sudut istimewa yaitu sudut yang mempunyai nilai sederhana. Karna itu kita perlu mengetahui nilai – nilai sudut istimewa yang terdapat pada tabel di bawah ini :
Tabel sudut istimewa

kita langsung masuk kesoal aja kali ya biar lebih enak, disini saya siapin beberapa conto soal mudah-mudahan kalian paham ya guys.
Contoh Soal 1 Limit Fungsi Triginometri (UN Matematika Tahun 2014)
Nilai dari
  \[ \lim_{x \rightarrow 1} \frac{\left( x^{2} - 1 \right) tan \left( 2x - 2 \right) }{sin^{2} \left( x - 1 \right) } = ... \]
Pembahasan:
Pertama, kita akan coba kerjakan menggunakan substitusi seperti yang dijelaskan pada tips mengerjakan limit.
  \[ \lim_{x \rightarrow 1} \frac{\left( x^{2} - 1 \right) tan \left( 2x - 2 \right) }{sin^{2} \left( x - 1 \right) } \]
  \[ = \frac{\left( 1^{2} - 1 \right) tan \left( 2(1) - 2 \right) }{sin^{2} \left( 1 - 1 \right) } \]
  \[ = \frac{0}{0} \]
Hasil akhir yang diperoleh bukan merupakan jawaban yang diharapkan, sehingga kita perlu mencari nilai limit yang tepat. Selanjutnya, gunakan metode pemfaktoran.
kumpulan soal limit fungsi trigonometri
Contoh Soal 2 Limit Fungsi Trigonometri
Tentukan nilai dari
  \[ \lim_{x \rightarrow \frac{\pi}{4}} \; \frac{cos \; 2x}{sin \; x - cos \; x} = ... \]
Pembahasan:
Soal yang diberikan pada soal dikerjakan dengan kombinasi pemfaktoran dan memanipulasi dengan identitas trigonometri. Identitas trigonometri yang digunakan adalah cosinus sudut rangkap, seperti terlihat pada persamaan di bawah.
  \[ cos \; 2x = cos^{2}x - sin^{2}x \]
Sekarang perhatikan proses pengerjaannya di bawah.
contoh soal limit fungsi trigonometri
Contoh Soal 4 Limiit Fungsi Trigonometri
Tentukan nilai dari limit di bawah!
  \[ \lim_{x \rightarrow \frac{\pi}{8}} \; \frac{sin^{2}2x - cos^{2}2x}{sin 2x - cos 2x} = .... \]
Pembahasan:
limit fungsi trigonometri
sekian aja ya pembahsan dari saya mengenai penjelasan dari limit trigonometri, pantengin terus blog saya intuk lrbih bnyak mengetahui apa aja yang terbaru. sekian dan terima kasih...semangat belajar guys



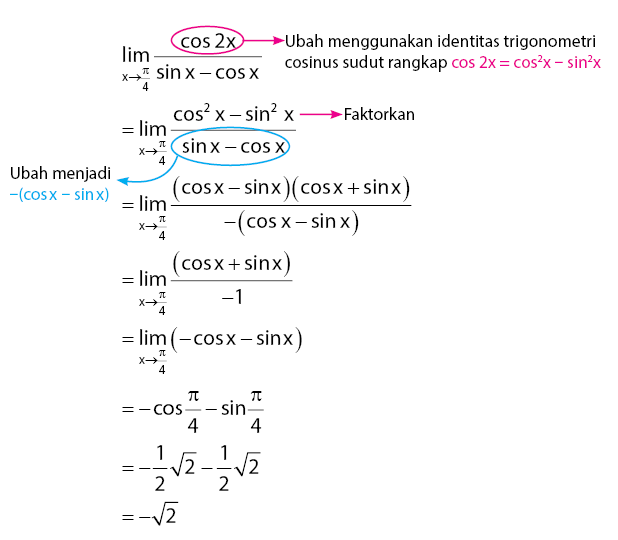
Komentar

Posting Komentar

Postingan populer dari blog ini

KALKULUS | BENTUK LIMIT TAK TENTU DENGAN ATURAN L'HOPITAL (PART 1)

-
Gambar
Bentuk Tak Tentu BAB 2 BENTUK TAK TENTU DAN INTEGRAL TAK WAJAR Bentuk Tak Tentu Pada limit fungsi trigonometri, telah dipelajari bahwa : Perhatikan bentuk limit ini untuk x→0, limit pembilang dan limit penyebutnya nol. Bentuk demikian dinamakan bentuk tak tentu 0/0. Kita mengenal tujuh macam bentuk tak tentu limit fungsi, yaitu : Pada bab ini kita hanya membahas empay bentuk yang pertama saja. Bentuk tak tentu lainnya melibatkan fungsi berpangkat fungsi, penyelesaiannya memerlukan konsep logaritma natural dan teorema L’Hospital. Permasalahan ini akan kita bahas pada penggunaan fungsi transenden dalam perhitungan limit fungsi. Berikut dua teorema penting untuk mempelajari limit-limit tak tentu : Berikut beberapa bentuk sekaligus contoh dalam integral tak tentu : 1.Bentuk tak tentu 0/0 : Cara penyelesaian :   Ubahlah bentuk f(x)/g(x) sehingga sifat-sifat limit fungsi dapat digunakan. Cara yang dapat dicoba adalah menguraikan pembilang dan penyebut,...
Baca selengkapnya

Yuk Belajar!! Determinan Matriks, metode ekspansi laplace dan determinan metode ekspansi laplace

-
Gambar
Belajar Tentang matriks yuk!! Determinan Matriks, Metode Ekspansi Laplace , Determinan Metode Ekspansi Laplace. Hai zulfirian, bagaimana kabarnya? Semoga selalu sehat dan tetap semangat belajar, ya! Apa jadinya dunia ini tanpa ilmu pengetahuan? Pernahkah para pemuda berpikir demikian? Dunia tanpa ilmu pengetahuan ibarat rumah tanpa lampu. Berkembangnya ilmu pengetahun tidak lepas dari peran para ilmuwan. Mereka rela menghabiskan waktu, tenaga, pikiran hanya untuk mengamati, memahami, dan menganalisis gejala alam di sekitar. Hal itu tentu tidak mudah, mengingat banyak variabel yang harus mereka pertimbangkan sebelum merumuskan ilmu pengetahuan yang baku dan bisa diterima semua orang. Saat menghadapi permasalahan dengan berbagai variabel, metode yang biasa digunakan adalah matriks. Hay sahabat,, hari ini kita akan melanjutkan kembali belajar matematika. Kali ini materi yang akan dibahas adalah Bagaimana Cara Menentukan Determinan Matriks, Metode ekspansi Laplace, Determ...
Baca selengkapnya

Matirks Metode OBE (operasi baris elementer)

-
Gambar
Matriks Metode OBE (Operasi Baris Elementer) Untuk menentukan solusi dari SPL dilakukan dengan cara membentuk matrik yang diperluas/diperbesar dari SPL dan melakukan Operasi Baris Elementer (OBE) pada matriks yang diperbesar tersebut. OBE ini didapatkan dalam suatu tahapan dengan menerapkan ketiga tipe operasi berikut untuk menghilangkan bilangan-bilangan tak diketahui secara sistematik. Kalikan persamaan dengan konstanta yang tak sama dengan nol. Pertukarkan dua persamaan tersebut. Tambahkan kelipatan dari satu persamaan bagi yang lainnya. Karena baris (garis horisontal) dalam matriks yang diperbesar beresuaian dengan persamaan dalam sistem yang diasosiasikan dengan baris tersebut, maka ketiga operasi ini bersesuaian dengan operasi berikut pada baris matriks yang diperbesar. Kalikanlah sebuah baris dengan sebuah konstanta yang taksama dengan nol. Pertukarkanlah dua baris tersebut. Tambahkanlah perkalian dari satu baris pada baris yang ...
Baca selengkapnya