PERTIDAKSAMAAN - ZULFI RAFIDHHOH HIKMI IT PLN

-
PERTIDAKSAMAAN
Pertidaksamaan adalah himpunan bilangan yang memenuhi sifat urutan bilangan tertentu. Pertidaksamaan dinyatakan dengan salah satu tanda dari lambang berikut : > ³ £ <.
(1)p < q artinya p lebih kecil dari pada q
(2)p > q artinya p lebih besar dari pada q
(3)p ≤ q artinya p lebih kecil atau sama dengan q
(4)p ≥q artinya p lebih besar atau sama dengan q

Sifat-sifat Sederhana :
(1)Penjumlahan/pengurangan.
   
   Jika x < y, maka x + a < y + a
   Misal, jika x < 10, mk x+2<10+2

(2)Perkalian/pembagian dengan bilangan positip. Untuk, a > 0,
  
   Jika x < y, maka ax < ay
    Misal, jika x < 2, mk 4x < 4(2)

(3)Perkalian/pembagian denan bilangan negatif. Untuk a < 0,
   Jika x < y, maka ax > ay
  Misal, jk x < 4, mk -2x > -2(4)

 Pertidaksamaan Sederhana
           Solusi pertidaksamaan adalah himpunan bilangan yang memenuhi pertidaksamaan. Solusinya dapat digambarkan pada garis bilangan.
           Contoh :
           Solusi dari : x + 4 > 7
           Ruas kiri dan kanan dikurangi 4 diperoleh,
           x + 4 – 4 > 7 – 4
                       x > 3
          Jadi semua nilai x lebih besar dari 3 yang memenuhi pertidaksamaan,
           
                                           →                                                     
          ---------+----+----+----+---------à x
                    0     1      2      3

             PERTIDAKSAMAAN KUADRAT
            Sama seperti pada persamaan kuadrat pada umumnya. Pangkat tertinggi pada pertidaksamaan kuadrat adalah 2 (dua). Perbedaan antara persamaan kuadrat dan pertidaksamaan kuadrat hanya terletak pada tanda penghubungnya. 
            

Menentukan Akar-Akar Pertidaksamaan Kuadrat

Langkah pertama untuk menentukan himpunan penyelesaian pertidaksamaan kuadrat adalah menentukan akar-akar pertidaksamaan kuadrat. Pada bagian awal telah disinggung bahwa cara menentukan akar-akar pertidaksamaan kuadrat sama dengan cara menentukan akar-akar persamaan kuadrat. Perbedaannya hanya dengan mengambil harga nol dari soal pertidaksamaan kuadrat yang diberikan.
Cara mengambil nilai nol dari pertidaksamaan kuadrat hanya dengan cara mengganti tanda pertidaksamaan menjadi tanda sama dengan. Sehingga diperoleh bentuk sementara berupa persamaan kuadrat. Sebagai contoh, perhatikan cara mengambil harga nol dari pertidaksamaan berikut ini.
Harga Nol
Cara yang sama juga berlaku untuk semua tanda pertidaksamaan.


            

Garis Bilangan dan Cara Menentukan Tanda pada Masing-Masing Daerah

Misalkan nilai akar-akar yang diperoleh dari perhitungan sebelumnya adalah a dan b. Maka garis bilangan yang dapat dibentuk dapat dilihat seperti gambar di bawah.
Garis bilangan pada pertidaksamaan kuadrat
Setelah dapat membentuk daerah garis bilangan seperti pada gambar di atas, berikutnya adalah menentukan nilai pada masing-masing daerah. Caranya adalah dengan mengambil satu titik uji pada suatu daerah.
            

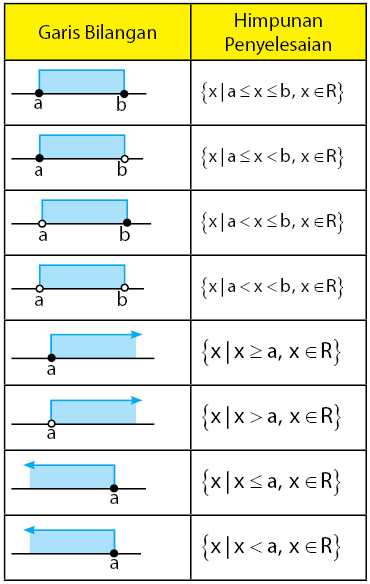
Himpunan Penyelesaian Pertidaksamaan Kuadrat

Hasil dari daerah yang memenuhi pertidaksamaan kuadrat biasanya disajikan dalam bentuk himpunan. Pada bagian ini, sobat idschool akan mempelajari cara menentukan notasi himpunan dari garis bilangan. Berikut ini adalah tabel cara membaca himpunan penyelesaian dari garis bilangan yang diberikan secara umum.
Himpunan Penyelesaian Pertidaksamaan Kuadrat
Untuk menambah pemahaman sobat terkait materi pertidaksamaan kuadrat. Berikut ini akan diberikan contoh soal cara menentukan himpunan penyelesaian pada pertidaksamaan kuadrat beserta dengan pembahasan nya.
Contoh 1: Soal Pertidaksamaan Kuadrat
Himpunan penyelesaian yang memenuhi pertidaksamaan kuadrat
  \[ x^{2} - x - 12 \leq 0 \]
Harga nol dari pertidaksamaan kuadrat x^{2} - x - 12 \geq 0 adalah x^{2} - x - 12 = 0. Selanjutnya akan ditentukan akar-akar persamaan kuadrat yang memenuhi.
  \[ x^{2} - x - 12 = 0 \]
  \[ \left(x + 3 \right) \left(x - 4 \right) = 0 \]
  \[ \left(x + 3 \right) = 0 \; \textrm{atau} \; \left(x - 4 \right) = 0 \]
  \[ x = - 3 \; \textrm{atau} \; x = 4 \]
Sehingga dapat diperoleh daerah pada garis bilangan dengan batas seperti gambar di bawah.
Garis Bilangan
Selanjutnya, akan diselidiki nilai dari masing-masing daerah.
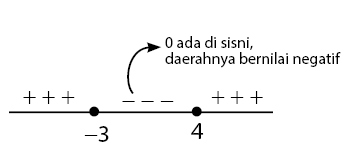
Ambil titik uji x = 0, kemudian substitusikan nilainya ke persamaan kuadrat
\[ 0^{2} - 0 - 12 = -12 \]
Untuk x = 0 menghasilkan nilai negatif, sehingga daerah yang memuat angka nol, daerahnya adalah negatif.
Contoh soal pertidaksamaan kuadrat
Pertidaksamaan kuadrat yang diberikan adalah x^{2} - x - 12 \geq 0, artinya himpunan penyelesaian dipenuhi untuk daerah yang bernilai positif.
Contoh soal cara menentukan himpunan penyelesaian pertidaksamaan kuadrat
Jadi himpunan penyelesaiannya adalah
  \[ \left \{ x \leq -3 \; \textrm{atau} \; x \geq 4 \right \} \]
           sekian pembahasan kita pada kali ini, tunggu untuk pembahasan materi selanjutnya. stay tune ya





Komentar

Posting Komentar

Postingan populer dari blog ini

KALKULUS | BENTUK LIMIT TAK TENTU DENGAN ATURAN L'HOPITAL (PART 1)

-
Gambar
Bentuk Tak Tentu BAB 2 BENTUK TAK TENTU DAN INTEGRAL TAK WAJAR Bentuk Tak Tentu Pada limit fungsi trigonometri, telah dipelajari bahwa : Perhatikan bentuk limit ini untuk x→0, limit pembilang dan limit penyebutnya nol. Bentuk demikian dinamakan bentuk tak tentu 0/0. Kita mengenal tujuh macam bentuk tak tentu limit fungsi, yaitu : Pada bab ini kita hanya membahas empay bentuk yang pertama saja. Bentuk tak tentu lainnya melibatkan fungsi berpangkat fungsi, penyelesaiannya memerlukan konsep logaritma natural dan teorema L’Hospital. Permasalahan ini akan kita bahas pada penggunaan fungsi transenden dalam perhitungan limit fungsi. Berikut dua teorema penting untuk mempelajari limit-limit tak tentu : Berikut beberapa bentuk sekaligus contoh dalam integral tak tentu : 1.Bentuk tak tentu 0/0 : Cara penyelesaian :   Ubahlah bentuk f(x)/g(x) sehingga sifat-sifat limit fungsi dapat digunakan. Cara yang dapat dicoba adalah menguraikan pembilang dan penyebut,...
Baca selengkapnya

Yuk Belajar!! Determinan Matriks, metode ekspansi laplace dan determinan metode ekspansi laplace

-
Gambar
Belajar Tentang matriks yuk!! Determinan Matriks, Metode Ekspansi Laplace , Determinan Metode Ekspansi Laplace. Hai zulfirian, bagaimana kabarnya? Semoga selalu sehat dan tetap semangat belajar, ya! Apa jadinya dunia ini tanpa ilmu pengetahuan? Pernahkah para pemuda berpikir demikian? Dunia tanpa ilmu pengetahuan ibarat rumah tanpa lampu. Berkembangnya ilmu pengetahun tidak lepas dari peran para ilmuwan. Mereka rela menghabiskan waktu, tenaga, pikiran hanya untuk mengamati, memahami, dan menganalisis gejala alam di sekitar. Hal itu tentu tidak mudah, mengingat banyak variabel yang harus mereka pertimbangkan sebelum merumuskan ilmu pengetahuan yang baku dan bisa diterima semua orang. Saat menghadapi permasalahan dengan berbagai variabel, metode yang biasa digunakan adalah matriks. Hay sahabat,, hari ini kita akan melanjutkan kembali belajar matematika. Kali ini materi yang akan dibahas adalah Bagaimana Cara Menentukan Determinan Matriks, Metode ekspansi Laplace, Determ...
Baca selengkapnya

Matirks Metode OBE (operasi baris elementer)

-
Gambar
Matriks Metode OBE (Operasi Baris Elementer) Untuk menentukan solusi dari SPL dilakukan dengan cara membentuk matrik yang diperluas/diperbesar dari SPL dan melakukan Operasi Baris Elementer (OBE) pada matriks yang diperbesar tersebut. OBE ini didapatkan dalam suatu tahapan dengan menerapkan ketiga tipe operasi berikut untuk menghilangkan bilangan-bilangan tak diketahui secara sistematik. Kalikan persamaan dengan konstanta yang tak sama dengan nol. Pertukarkan dua persamaan tersebut. Tambahkan kelipatan dari satu persamaan bagi yang lainnya. Karena baris (garis horisontal) dalam matriks yang diperbesar beresuaian dengan persamaan dalam sistem yang diasosiasikan dengan baris tersebut, maka ketiga operasi ini bersesuaian dengan operasi berikut pada baris matriks yang diperbesar. Kalikanlah sebuah baris dengan sebuah konstanta yang taksama dengan nol. Pertukarkanlah dua baris tersebut. Tambahkanlah perkalian dari satu baris pada baris yang ...
Baca selengkapnya